二分法查找是一种基于比较目标值和数组中间元素的算法
- 如果目标值 = 中间值,则找到目标值
- 如果目标值 < 中间值,则在左侧继续搜索
- 如果目标值 > 中间值,则在右侧继续搜索
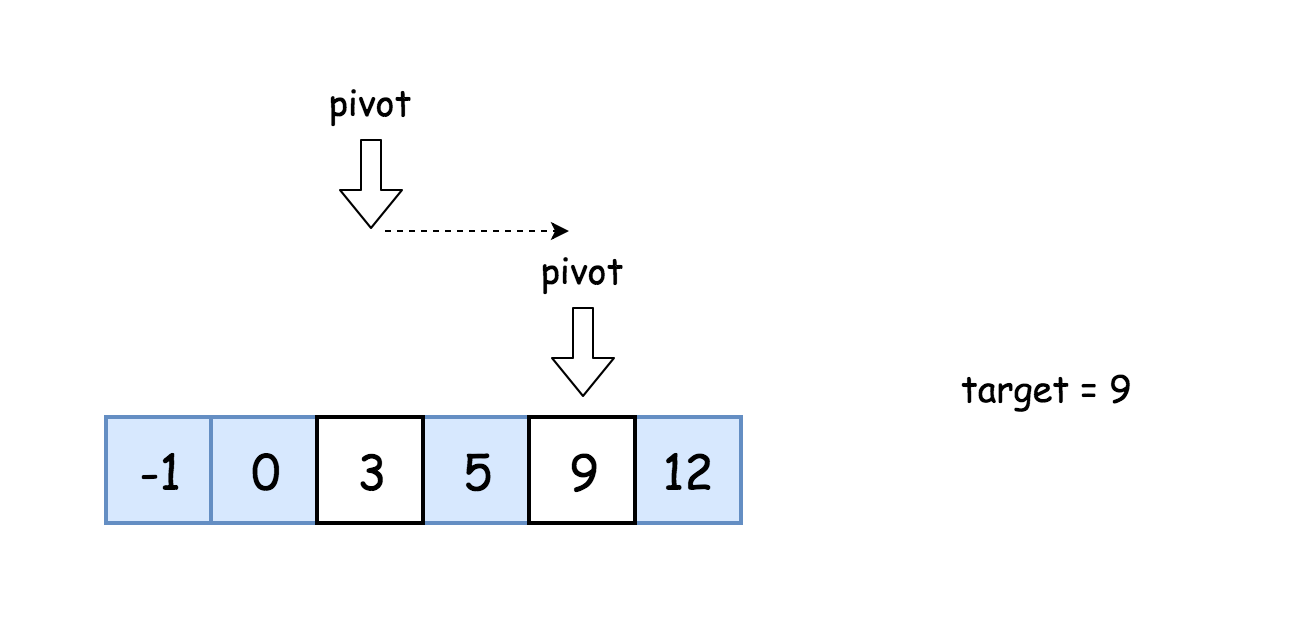
解题思路:
- 初始化指针left = 0, right=n-1;
- 当left <= right:
- 比较中间元素nums[pivot]和目标值target
1.target = nums[pivot], 返回pivot
2.target > nums[pivot], 则在右侧继续搜索left = pivot+1
3.target < nums[pivot], 则在左侧继续搜索right = pivot+1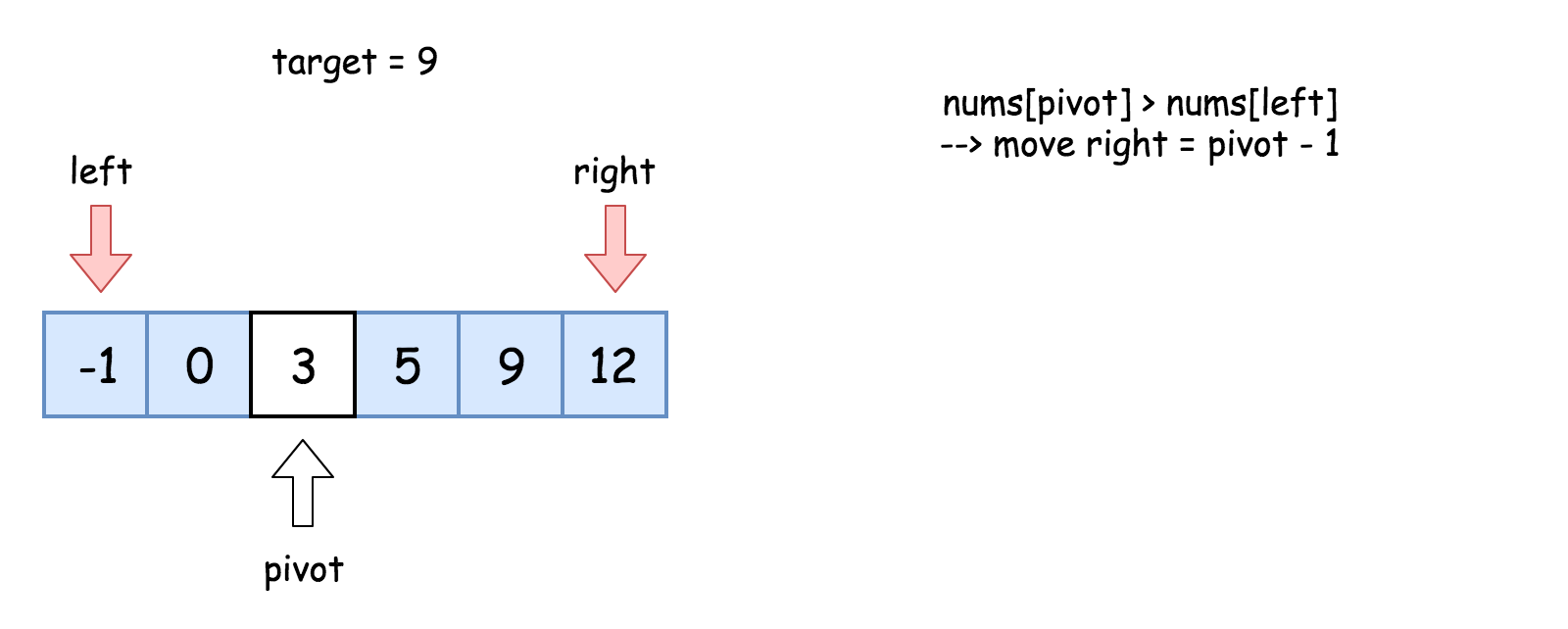
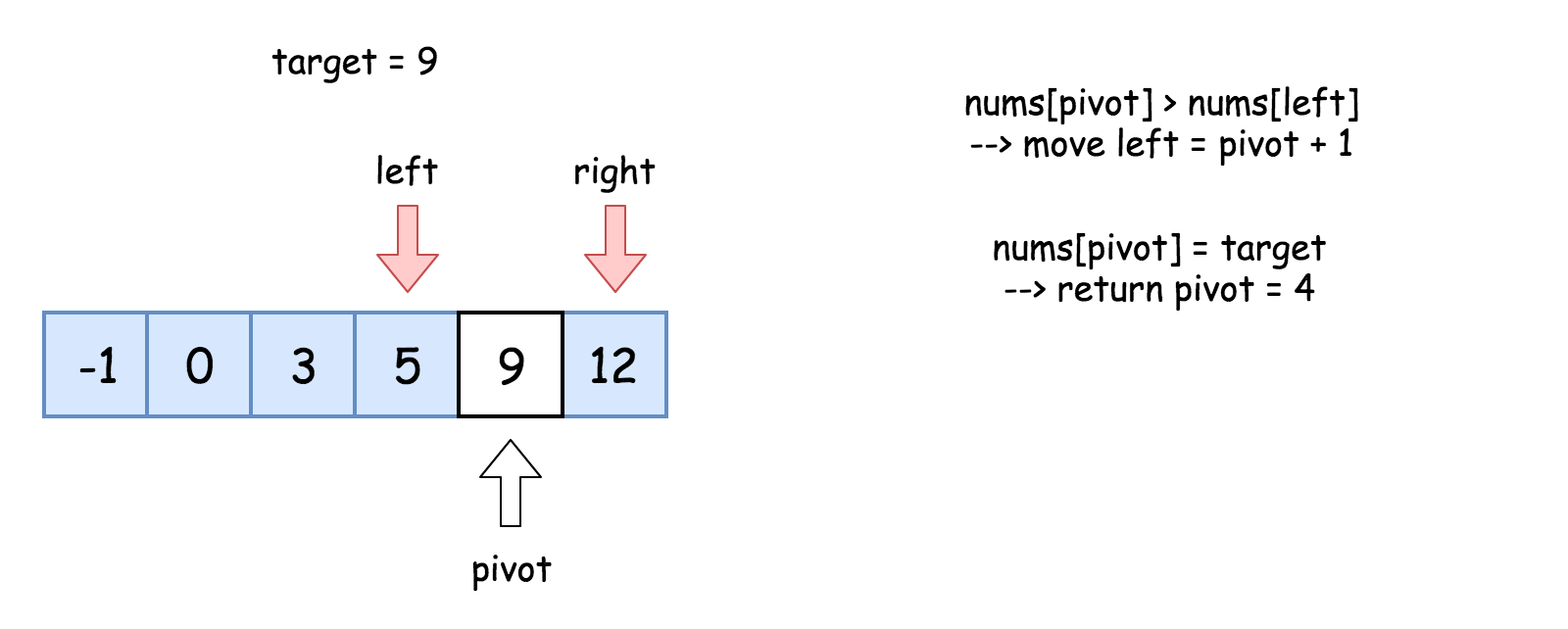
- 比较中间元素nums[pivot]和目标值target
1 | /** |
复杂度分析:
- 时间复杂度:O(logN)
- 空间复杂度:O(1)


