快速排序 Quick Sort

1. 前言

基本思想：选择一个基准数，通过一趟排序将要排序的数据分割成独立的两部分；其中一部分的所有数据都比另外一部分的所有数据都要小。然后，再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列

2. 实现

1. 从数列中挑出一个基准值

2. 将所有比基准值小的摆放在基准前面，所有比基准大的放基准后面（相同的可以放任意边）；在这个分区推出后，该基准就处于数列的中间位置

3. 递归把基准前面的子数列 和基准后面的子数列进行排序

下面以数列a = {30,40,60,10,20,50}为例，演示它的快速排序过程：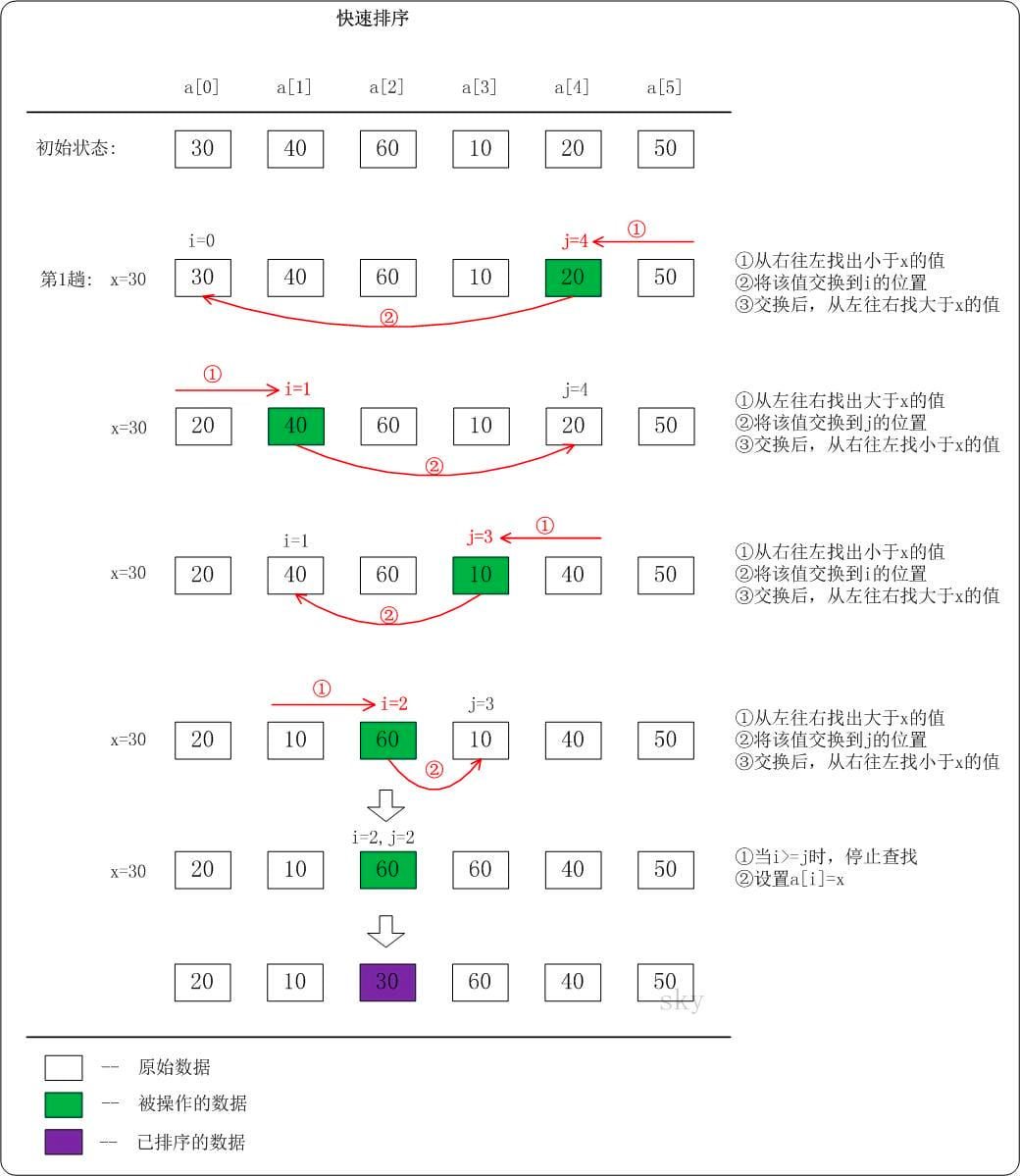

上图只是给出了第1趟快速排序的流程。在第1趟中，设置x=a[i]，即x=30。

• 从”右 –> 左”查找小于x的数: 找到满足条件的数a[j]=20，此时j=4；然后将a[j]赋值a[i]，此时i=0；接着从左往右遍历。
• 从”左 –> 右”查找大于x的数: 找到满足条件的数a[i]=40，此时i=1；然后将a[i]赋值a[j]，此时j=4；接着从右往左遍历。
• 从”右 –> 左”查找小于x的数: 找到满足条件的数a[j]=10，此时j=3；然后将a[j]赋值a[i]，此时i=1；接着从左往右遍历。
• 从”左 –> 右”查找大于x的数: 找到满足条件的数a[i]=60，此时i=2；然后将a[i]赋值a[j]，此时j=3；接着从右往左遍历。
• 从”右 –> 左”查找小于x的数: 没有找到满足条件的数。当i>=j时，停止查找；然后将x赋值给a[i]。

此趟遍历结束！按照同样的方法，对子数列进行递归遍历。最后得到有序数组

3. 时间复杂度和稳定性

• 稳定性：不稳定算法（假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的）

• 时间复杂度：快速排序的时间复杂度在最坏情况下是O(N2)，平均的时间复杂度是O(N*logN)。

4. 代码实现

public class QuickSort {

    /**
     * 快速排序
     * @param a 带排序的数组
     * @param l 左边界
     * @param r 右边界
     */
    public static void quickSort(int[] a, int l, int r) {
        if (l < r) {
            int i, j, x;

            i = l;
            j = r;
            x = a[i];
            while (i < j) {
                while (i < j && a[j] > x) {
                    j--; //从右往左找第一个小于x的数
                }
                if (i < j) {
                    a[i++] = a[j];
                }
                while (i < j && a[i] > x) {
                    j--; //从左往右找第一个大于x的数
                }
                if (i < j) {
                    a[j--] = a[i];
                }
            }
            a[i] = x;
            quickSort(a, l, i - 1);
            quickSort(a, i + 1, r);
        }
    }

    public static void main(String[] args) {
        int[] a = {20,40,30,10,60,50};
        quickSort(a, 0, a.length - 1);
        for (int i = 0; i < a.length; i++) {
            System.out.printf("%d ", a[i]);
        }
    }
}