树 - 前缀树 Trie Tree

10 Algorithm 评论

Trie又称字典树、单词查找树或者键树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计、排序和保存大量的字符串（但不限于），所以经常被搜索引擎系统用于文本词频统计。

优点：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高

1. 定义

在计算机科学中，trie又称前缀树或者字典树，是一种有序树，用于保存关联数组，其中的键通常是子夫唱。与二叉查找树不同，键不是直接保存在节点中，而是有节点在树中的位置决定。一个节点的所有子孙都有相同的前缀，也就是这个节点对应的字符串，而根节点对应空字符串。

一般情况下，不是所有节点都有对应的值，只有叶子节点和部分内部节点所对应的键才有相关的值。

Trie中的键通常是字符串，但也可以是其他的结构。trie的算法可以很容易地修改为处理其他结构的有序序列，比如一串树姿或者形状的排列。比如bitwise trie中的键是一串位元，可以用于表示整数或者内存地址。trie树常用于搜索提示。如当输入一个网址，可以自动搜索出可能的选择。当没有完全匹配的搜索结构，可以返回前缀最相似的可能。

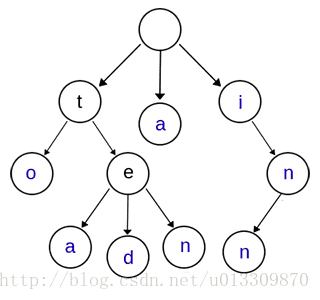
上图中是一棵Trie树，表示了关键字集合{“a”,”to”,”tea”,”ted”,”ten”,”i”,”in”,”inn”}.从上图可以归纳出Trie树的基本性质：

  • 根节点不包含字符串，出根节点外每个节点都包含一个字符

  • 从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串

  • 每个节点的所有子节点包含的字符互不相同

  • 从第一个字符开始有连续重复的字符只占用一个节点，比如上面的to、ten中重复的单词t只占用了一个节点

2. 前缀树的实现

重点在于节点数据结构，重要的插入和查找方法，以及递归和非递归两种形式

2.1 节点数据结构定义

Node节点中使用Map较为搞笑，用于映射到下一个节点：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * @author xiaoyuge
 */
public class Trie {
    class Node {
        public boolean isWord;//  是否是某个单词的结束
        public TreeMap<Character, Node> next;//到下一个节点的映射

        public Node(boolean isWord) {
            this.isWord = isWord;
            next = new TreeMap<>();//初始化
        }

        public Node() {
            this(false);
        }
    }
    /**
     * 根节点
     */
    private Node root;
    /**
     * Trie单词的个数
     */
    private int size;
    public Trie() {
        root = new Node();
        size = 0;
    }
    /**
     * 获取Trie中存储的单词数量
     */
    public int getSize() {
        return size;
    }
}

2.2 插入方法

非递归方式

向Trie中添加一个新的单词word，将单词拆分成一个个字符c，然后从根节点往下添加

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public void add(String word) {
    Node cur = root;
    //循环判断新的cur节点是否包含下一个字符串到下一个节点的映射
    for (int i = 0; i < word.length(); i++) {
        //将c当成一个节点插入Trie中
        char c = word.charAt(i);
        //判断cur.next是不是已经指向我们要找的c字响应的节点
        if (cur.next.get(c) != null) {
            //新建节点
            cur.next.put(c, new Node());
        }
        //否则，就直接走到该节点的为止
        cur = cur.next.get(c);
    }
    if (!cur.isWord) {
        //确定cur是新的单词
        cur.isWord = true;
        size++;
    }
}

递归方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * 向Trie中添加一个新的单词word(递归写法接口)
 * @param word
 */
public void recursionAdd(String word){
    Node cur = root;
    add(root, word, 0);
}
/**
 * 递归
 * @param node  要添加的节点
 * @param word  要添加的单词
 * @param index
 */
public void add(Node node, String word, int index) {
    //确定终止条件，这个终止条件在没加index这个参数时，很难确定
    //此时一个单词已经遍历完成了，如果这个结束节点没有标记为单词，就标记为单词
    if (!node.isWord && index == word.length()) {
        node.isWord = true;
        size++;
    }
    if (word.length() > index) {
        char addLetter = word.charAt(index);
        //判断trie的下个节点租种是否有查询的字符，如果没有，就添加
        if (node.next.get(addLetter) == null) {
            node.next.put(addLetter, new Node());
        }
        //基于已经存在的字符进行下个字符的递归查询
        add(node.next.get(addLetter), word, index + 1);
    }
}

2.3 查询单词方法

非递归方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/**
 * 查询单词word是否在Trie中
 */
public boolean contains(String word) {
    Node cur = root;
    for (int i = 0; i < word.length(); i++) {
        char c = word.charAt(i);
        if (cur.next.get(c) == null) {
            return false;
        } else {
            cur = cur.next.get(c);
        }
    }
    return cur.isWord;
}

递归方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public boolean recursionContains(String word) {
    Node cur = root;
    return contains(root, word, 0);
}

/**
 * 查询word中是否在Trie中递归写法
 * @param node
 * @param word
 * @param index
 * @return
 */
private boolean contains(Node node, String word, int index) {
    if (index == word.length()) {
        return node.isWord;
    }
    char c = word.charAt(index);
    if (node.next.get(c) == null) {
        return false;
    } else {
        return contains(node.next.get(c), word, index + 1);
    }
}

2.4 查询前缀方法

非递归方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * 查询是否在Trie中有单词 - prefix为前缀
 */
public boolean isPrefix(String prefix){
    Node cur = root;
    for (int i = 0; i < prefix.length(); i++) {
        char c = prefix.charAt(i);
        if (cur.next.get(c) == null){
            return false;
        }
        cur = cur.next.get(c);
    }
    return true;
}

递归方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public boolean recursionIsPrefix(String prefix) {
    Node node = root;
    return recursionIsPrefix(root, prefix, 0);
}

/**
 * 查询是否在Trie中有单词一prefix为前缀(递归实现)
 */
public boolean recursionIsPrefix(Node root, String prefix, int index) {
    if (prefix.length() == index) {
        return true;
    }
    char c = prefix.charAt(index);
    if (root.next.get(c) == null) {
        return false;
    }
    return recursionIsPrefix(root.next.get(c), prefix, ++index);
}

3. 前缀树拓展

3.1 前缀树的复杂度

设平均查询的query词长为n，白名单m条记录，平均长度k：

  • 简单单词查询：一个query，需要遍历每一个白名单，调用query是否contains方法，contains方法遍历前词，找到头元素一致，再遍历判断尾序列，contains的复杂度O(n)，整体复杂度O(mn)
  • 前缀树查询：一个query，将这个query从头遍历到尾，每个元素在前缀树中判断，操作都是取下一个节点和判断是否为end，时间复杂度为O(1)，整体时间复杂度是O(n)

3.2 前缀树有哪些应用

  • 前缀匹配

  • 字符串检索，比如敏感词过滤，黑白名单等

  • 词频统计

  • 字符串排序

3.3 前缀树的压缩：基数树

在计算机科学中，基数树，或称压缩前缀树，是一种更节省空间的 Trie（前缀树）。对于基数树的每个节点，如果该节点是确定的子树的话，就和父节点合并。基数树可用来构建关联数组。 用于 IP 路由。 信息检索中用于文本文档的倒排索引

基数树可看做是以二进制位串为关键字的 trie 树，是一种多叉树形结构，同时又类似多层索引表，每个中间节点包含指向多个子节点的指针数组，叶子节点包含指向实际的对象的指针(由于对象不具备树节点结构，因此将其父节点看做叶节点)。基数树也被设计成多道树，以提高磁盘交互性能。同时，基数树也是按照字典序来组织叶节点的，这种特点使之适合持久化改造，加上它的多道特点，灵活性较强，适合作为区块链的基础数据结构，构建持久性区块时较好地映射各类数据集合上。基数树支持插入、删除、查找操作。查找包括完全匹配、前缀匹配、前驱查找、后继查找。所有这些操作都是 O(k)复杂度，其中 k 是所有字符串中最大的长度

4. 参考文章

小余哥xiaoyouge

分享一些技术教程与实践，以及日常踩坑记录。