1. BST的定义
在二叉查找树中:
若任意结点的左子树不空,则左子树上所有的结点的值均小于根结点的值;
若任意结点的右子树不空,则右子树上所有的结点的值均小于根结点的值;
任意结点的左、右子树也分别为二叉查找树
没有键值相等的结点

动画效果请参考【BST】
2. BST的实现
2.1 结点
BSTree是二叉树,它保存了二叉树的根节点mRoot;mRoot是BSTNode类型,而BSTNode是二叉查找树的节点,它是BSTree的内部类。BSTNode包含二叉查找树的几个基本信息:
key:关键字,用来对二叉查找树的节点进行排序left:指向当前节点的左子树right:指向当前节点的右子树parent:指向当前节点的父节点
1 | /** |
2.2 遍历
2.2.1 前序遍历
若二叉树非空,则执行以下操作:
访问根节点
先序遍历左子树
先序遍历右子树
1 | /** |
2.2.2 中序遍历
若二叉树非空,则执行以下操作:
中序遍历左子树
访问根节点
中序遍历右子树
1 | /** |
2.2.3 后序遍历
若二叉树非空,则执行以下操作:
后序遍历左子树
后序遍历右子树
访问根节点
1 | /** |
2.2.4 测试
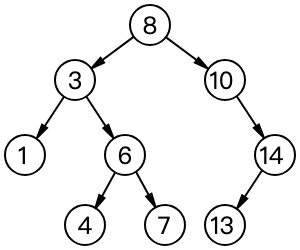
对于上面的二叉树而言:
前序遍历:8,3,1,6,3,7,10,14,13
中序遍历:1,3,6,4,7,8,10,13,14
后序遍历:1,4,7,6,3,13,14,10,8
2.3 查找
递归版本代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22/**
* 递归实现查找"二叉树 X"中键值为 key 的节点
*/
private BSTNode<T> search(BSTNode<T> x, T key){
if (x == null){
return x;
}
int cmp = key.compareTo(x.key);
if (cmp < 0){
//key在左子树上
return search(x.left, key);
}else if(cmp > 0){
//key 在右子树上
return search(x.right, key);
}else{
return x;
}
}
public BSTNode<T> search(T key){
return search(mRoot, key);
}非递归版本的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19/**
* 非递归实现查找"二叉树 X"中键值为 key 的节点
*/
private BSTNode<T> iterativeSearch(BSTNode<T> x, T key){
while (!(null == x)){
int cmp = key.compareTo(x.key);
if (cmp < 0){
x = x.left;
}else if(cmp > 0){
x = x.right;
}else{
return x;
}
}
return x;
}
public BSTNode<T> iterativeSearch(T key){
return iterativeSearch(mRoot, key);
}
2.4 最大值和最小值
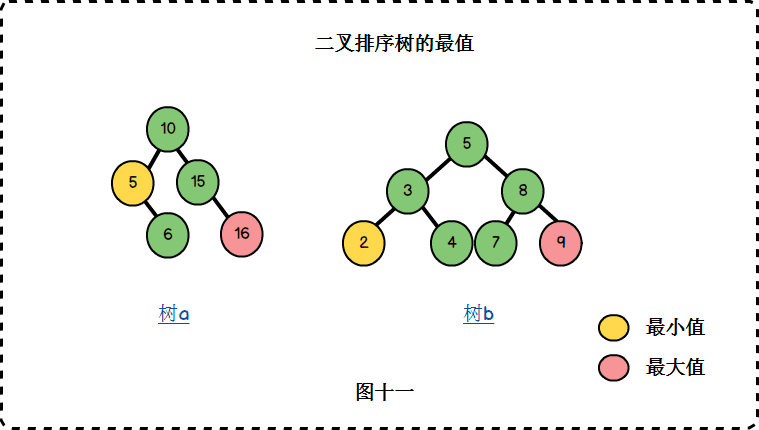
查找最大值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21/**
* 查找最大结点:返回tree为根节点的二叉树的最大结点
* 最大结点永远在右子树上
*/
private BSTNode<T> maximum(BSTNode<T> tree){
if (tree == null){
return null;
}
while (tree.right != null){
tree = tree.right;
}
return tree;
}
public T maximum(){
BSTNode<T> p = maximum(mRoot);
if (p != null){
return p.key;
}
return null;
}查找最小值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20/**
* 查找最小结点:返回tree为根节点的二叉树的最小结点
* 最小结点永远在左子树上
*/
private BSTNode<T> minimum(BSTNode<T> tree) {
if (tree == null) {
return null;
}
while (tree.left != null){
tree = tree.left;
}
return tree;
}
public T minimum(){
BSTNode<T> p = minimum(mRoot);
if (p != null){
return p.key;
}
return null;
}
2.5 前驱后继
结点的前驱:是该结点左子树中最大结点。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18/**
* 找结点(x)的前驱结点。即,查找"二叉树中数据值小于该结点"的"最大结点"。
*/
public BSTNode<T> predecessor(BSTNode<T> x) {
//如果x存在左子树,则"x的前驱结点"为:以其左子树根的子树的最大结点
if (x.left != null) {
return maximum(x.left);
}
// 如果x没有左孩子。则x有以下两种可能:
//1. x是"一个右孩子",则"x的前驱结点"为 "它的父结点"。
//2. x是"一个左孩子",则查找"x的最低的父结点,并且该父结点要具有右孩子",找到的这个"最低的父结点"就是"x的前驱结点"。
BSTNode<T> y = x.parent;
while ((y != null) && (x == y.left)) {
x = y;
y = y.parent;
}
return y;
}
结点的后继:是该结点的右子树上最小的结点1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18/**
* 找结点(x)的后继结点。即,查找"二叉树中数据值大于该结点"的"最小结点"。
*/
public BSTNode<T> successor(BSTNode<T> x) {
// 如果x存在右孩子,则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。
if (x.right != null) {
return minimum(x.right);
}
// 如果x没有右孩子。则x有以下两种可能:
// 1. x是"一个左孩子",则"x的后继结点"为 "它的父结点"。
// 2. x是"一个右孩子",则查找"x的最低的父结点,并且该父结点要具有左孩子",找到的这个"最低的父结点"就是"x的后继结点"。
BSTNode<T> y = x.parent;
while ((y != null) && (x == y.right)) {
x = y;
y = y.parent;
}
return y;
}
2.6 插入
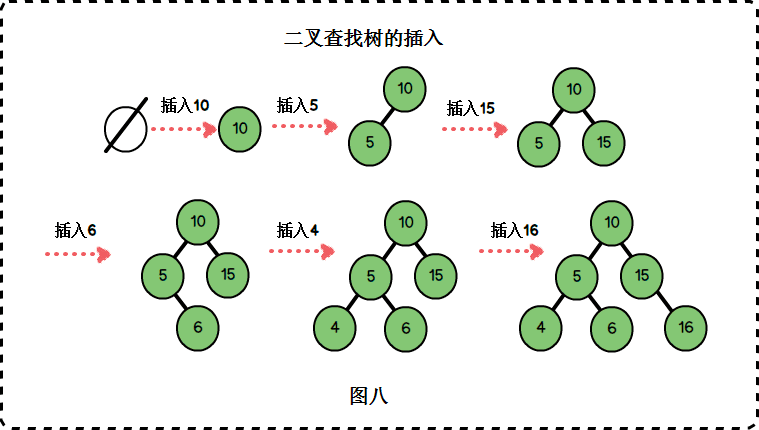
1 | /** |
2.7 删除
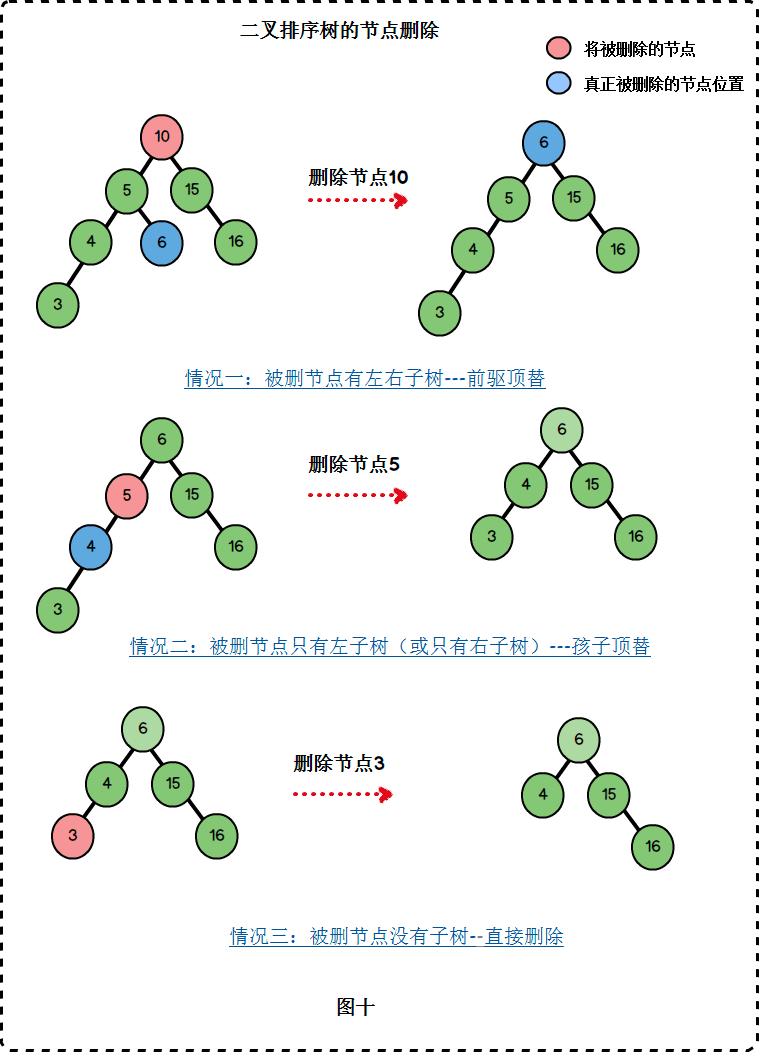
1 | /** |
2.8 打印树
1 | /** |
2.9 销毁
1 | /** |
3. 完整代码示例
1 | /** |
4. 测试程序
下面对测试程序的流程进行分析:
新建二叉树root
向二叉树中依次加入1,5,4,3,2,6。如图所示:

Java代码测试:
1 | /** |
运行后输出:
1 | ---- 依次添加:154326 |
5. 参考文章
本文主要来源于@pdai的https://pdai.tech/md/algorithm/alg-basic-tree-search.html,在此基础上重新组织和增加了内容。


