Shell排序 Shell Sort

1. 前言

希尔排序实际上是一种分组插入方法。它的基本思想是: 对于n个带排序的数列，去一个小于n的整数gap(gao被称为步长)将待排序元素分成若干个组子序列，所有距离为gap的倍数的记录放在同一个
组中；然后，对各组内的元素进行直接插入排序。这一趟排序完成之后，每一个组的元素都是有序的。然后减少gap值，并重复执行上述的分组和排序。重复这样的操作，当gap=1时，整个数列就是有序的。

2. 实现

下面以数列{80,30,60,40,20,10,50,70}为例演示它的希尔排序过程：

1. 第一趟：gap = 4
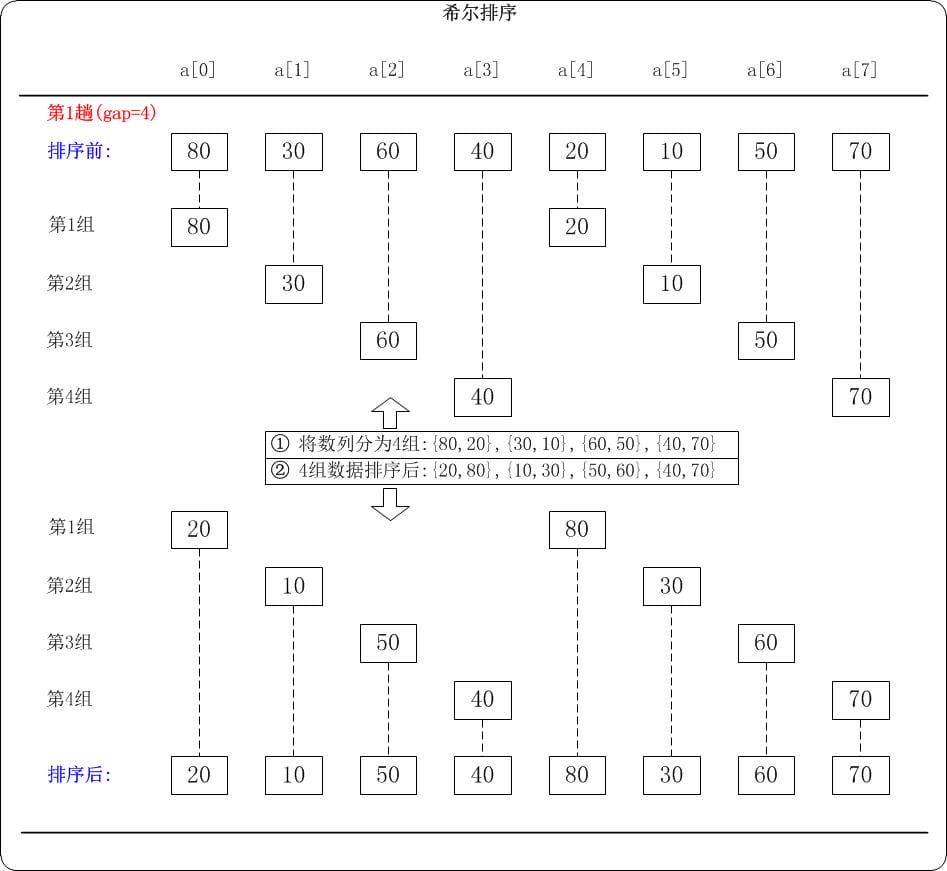   当gap=4时，意味着将数列分成4个组：{80,20},{30,10},{60,50},{40,70};对应数列：{80,30,60,40,20,10,50,70},对这4个组分别进行排序，排序的结果是：{20,80},{10,30},{50,60},{40,70}

2. 第二趟：gap = 2

   

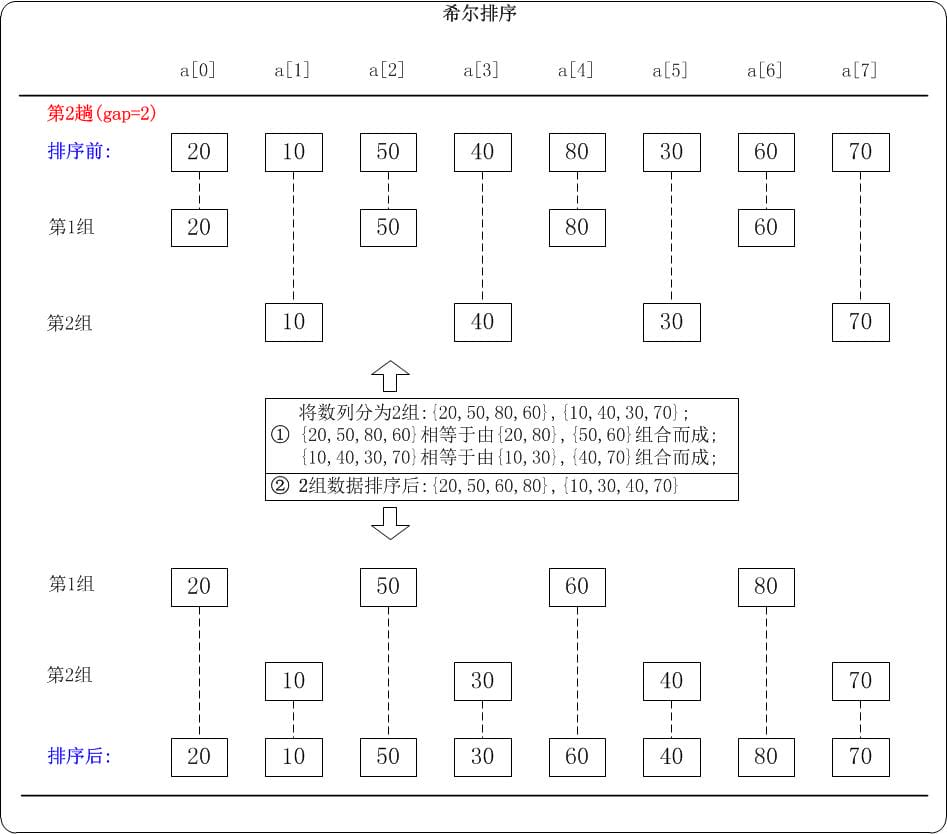
   当gap=2时，意味着将薯类分成2个组：{20,50,80,60}、{10,40,30,70}，对应数列：{20,10,50,40,80,30,60,70}；注意{20,50,80,60}实际上是由两个有序数列{20,80}和{50,60}组成的。{10,40,30,70}实际上有两个有序的数列{10,30}和{40,70}组成。对这2个组分别进行排序，排序结果: {20,50,60,80}, {10,30,40,70}。

3. 第三趟：gap = 1

   

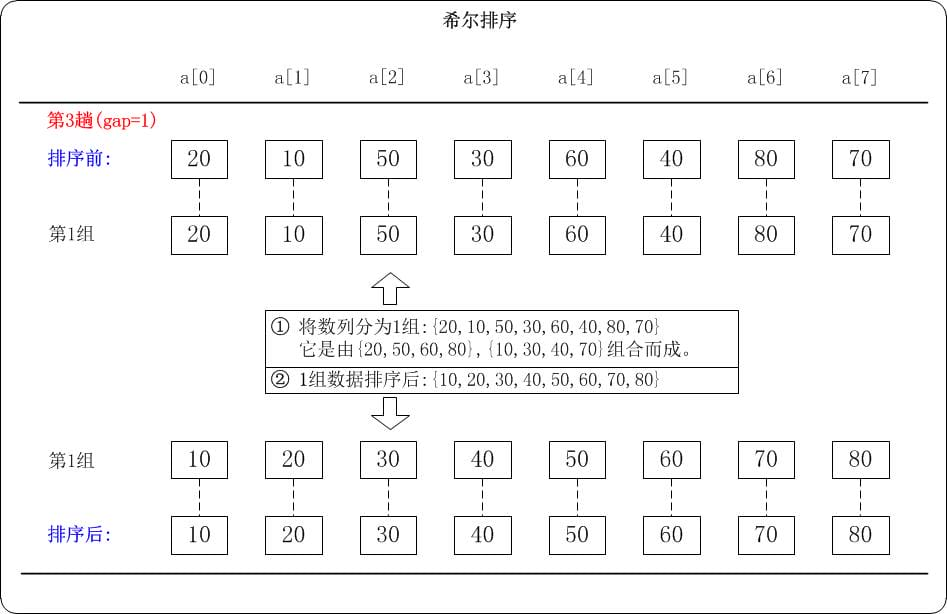
   当gap=1时,意味着将数列分为1个组: {20,10,50,30,60,40,80,70} 注意: {20,10,50,30,60,40,80,70}实际上有两个有序的数列{20,50,60,80}和{10,30,40,70}组成。 对这1个组分别进行排序

3. 时间复杂度和稳定性

• 时间复杂度：希尔排序的时间复杂度与增量(即，步长gap)的选取有关。例如，当增量为1时，希尔排序退化成了直接插入排序，此时的时间复杂度为O(N²)，而Hibbard增量的希尔排序的时间复杂度为O(N3/2)

• 稳定性：希尔排序是按照不同步长对元素进行插入排序，当刚开始元素很无序的时候，步长最大，所以插入排序的元素个数很少，速度很快；当元素基本有序了，步长很小， 插入排序对于有序的序列效率很高。所以，希尔排序的时间复杂度会比O(n^2)好一些。由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的

4. 代码实现

package org.example.sort;

public class ShellSort {

    public static void shellSort(int[] a) {
        //gap步长：每次减为原来的一般
        for (int gap = a.length / 2; gap > 0; gap /= 2) {
            //共gap个组，对每一个组都执行插入排序
            for (int i = 0; i < gap; i++) {
                for (int j = i + gap; j < a.length; j += gap) {
                    // 如果a[j] < a[j-gap]，则寻找a[j]位置，并将后面数据的位置都后移。
                    if (a[j] < a[j - gap]) {
                        int tmp = a[j];
                        int k = j - gap;
                        while (k >= 0 && a[k] > tmp) {
                            a[k + gap] = a[k];
                            k -= gap;
                        }
                        a[k + gap] = tmp;
                    }
                }
            }
        }
    }

    /**
     * 对希尔排序中的单个组进行排序
     * a -- 待排序的数组
     * n -- 数组总的长度
     * i -- 组的起始位置
     * gap -- 组的步长
     * 组是"从i开始，将相隔gap长度的数都取出"所组成的！
     */
    public static void groupSort(int[] a, int n, int i, int gap) {
        for (int j = i + gap; j < n; j += gap) {
            // 如果a[j] < a[j-gap]，则寻找a[j]位置，并将后面数据的位置都后移。
            if (a[j] < a[j - gap]) {
                int tmp = a[j];
                int k = j - gap;
                while (k >= 0 && a[k] > tmp) {
                    a[k + gap] = a[k];
                    k -= gap;
                }
                a[k + gap] = tmp;
            }
        }
    }

    /**
     * 希尔排序
     * a -- 待排序的数组
     * n -- 数组的长度
     */
    public static void shellSort2(int[] a, int n) {
        // gap为步长，每次减为原来的一半。
        for (int gap = n / 2; gap > 0; gap /= 2) {
            // 共gap个组，对每一组都执行直接插入排序
            for (int i = 0; i < gap; i++) {
                groupSort(a, n, i, gap);
            }
        }
    }
    public static void main(String[] args) {
        int i;
        int a[] = {80,30,60,40,20,10,50,70};
        shellSort(a);
        for (i=0; i<a.length; i++) {
            System.out.printf("%d ", a[i]);
        }
        System.out.printf("\n");
    }
}